Использование ИИ для решения задач Международной математической олимпиады с помощью методов математического анализа.

Математическое моделирование с помощью ИИ: прорыв в решении сложных задач

Представьте, что у вас есть мощный компьютер, который может решать сложные математические задачи. Но, чтобы он смог правильно решить эти задачи, ему нужно указать, как это сделать. Это как найти путь в неизвестном городе: вам нужно дать компьютеру «карту», по которой он сможет пройти.

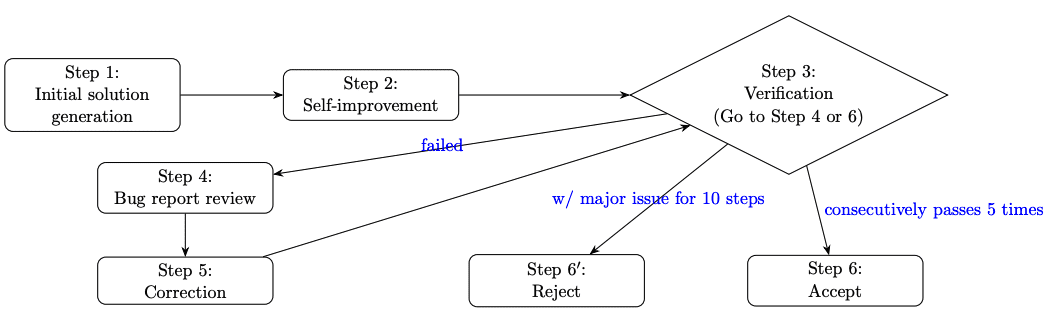
Китайские исследователи сделали именно это, используя мощную модель Google Gemini 2.5 Pro для решения задач Международной математической олимпиады (IMO). Они разработали специальный пайплайн для решения математических задач, который включает несколько этапов: генерация начального решения, самосовершенствование модели, верификация решения и исправление ошибок.

Одним из ключевых моментов в этом процессе является строгость. Каждый шаг должен быть логически обоснован, чтобы избежать ошибок. Например, если вы пытаетесь решить задачу о конфигурации прямых на плоскости, вам нужно тщательно проанализировать все возможные варианты и исключить те, которые не удовлетворяют заданным условиям. Применение ИИ в математических исследованиях открывает новые возможности для решения таких задач.

Использование верстки TeX для математических выражений также очень важно. Это как использовать специальный язык для описания математических формул, который позволяет компьютеру понять и обработать их правильно. Роль верификатора в математическом рассуждении также очень важна. Он проверяет решение на наличие ошибок и классифицирует их на критические и пробелы в обосновании.

Исследователи применили эту модель к задачам IMO 2025 и получили очень хорошие результаты. Они смогли решить пять из шести задач, что является очень высоким результатом. Это показывает, что с правильной методологией современные модели ИИ могут достигать уровня, сопоставимого с медалистами математических олимпиад. Разработка пайплайна для решения математических задач является ключевым фактором в этом успехе.

Одним из примеров успешного решения задачи является задача о комбинаторной геометрии. Модель смогла определить все возможные конфигурации прямых на плоскости и доказать, что только три из них удовлетворяют заданным условиям. Это было достигнуто путем тщательного анализа ограничений на пересечения и использованием свойств «солнечных» прямых. Применение методов математического анализа и дискретной оптимизации в ИИ также сыграло важную роль в этом успехе.

В целом, результаты исследования показывают, что мощные существующие модели уже способны решать сложные задачи математического рассуждения, но прямое их использование может приводить к плохим результатам. Разработанный подход показывает значительный прогресс в математическом моделировании с помощью ИИ, открывая новые возможности для применения ИИ в математических исследованиях и образовании.

Больше новостей в нашем телеграм канале I ROBOT